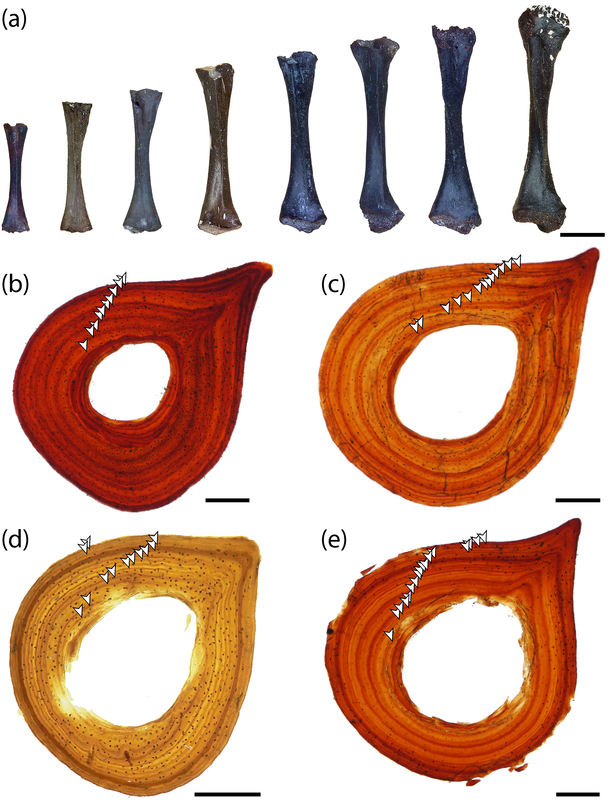
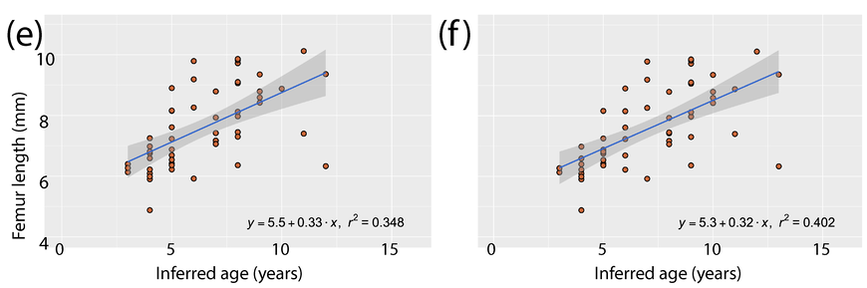
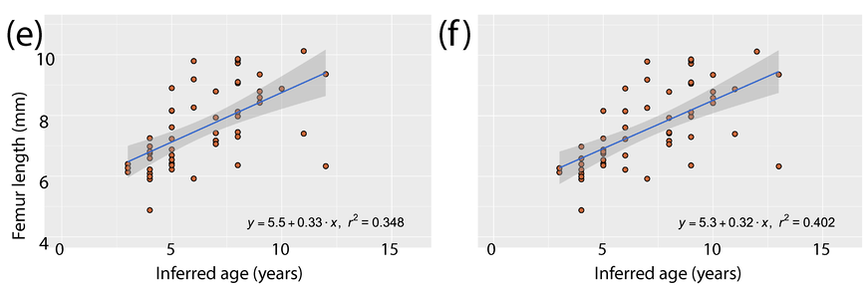
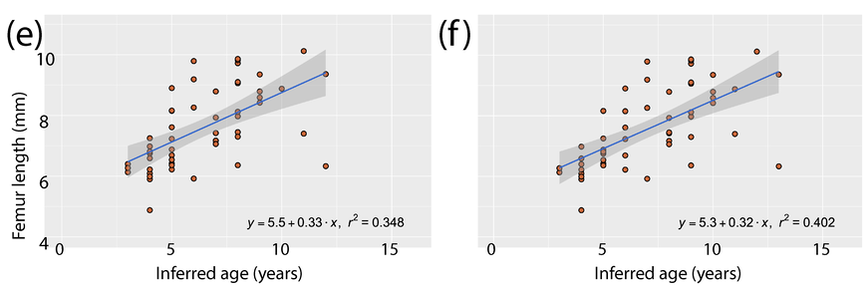
Here's the most detailed illustrations ever published of a Doleserpeton femur. They were done by a former ROP/BIO481 student in our lab in 2017, Paige Urban, who is now a vet student at Guelph! We used this and previous publications as a reference for identifying limb bones of Doleserpeton to sample; they can be pretty well identified by their slenderness and the prominent trochanter; similarly sized limbs of dissorophoids that reached much larger adult body sizes wouldn't be this well-ossified at a size that would probably be within the first few months of life, whereas this sized limb in Doleserpeton could belong to an individual more than 10 years old. The methods Pretty standard histology methods - embed specimens, cut them, glue them to slides, grind them down to be imaged under a microscope. Read the paper if you want the nitty-gritty on equipment, etc. I will just point out that these are really small - the scale bar in Part A is 2 mm, and the scale bar for Parts B-E is 0.25 mm. Then we went through and counted lines of arrested growth (LAGs), which are marked by distinctive bands extending around the circumference of the bone. The arrows in the above thin sections mark those lines that we counted. The difficult part came when we were making interpretations of the LAGs - does each one represent a year of growth, or is it a different periodicity. Based on the clumping of LAGs in pairs of closely spaced lines, with more space from the adjacent pair than between the pair, we interpreted that a lot of these have what are called "double LAGs," or where a pair represents two periods of the year in which growth was unfavourable. Part C above has some particularly clear double LAGs. We then plotted the inferred age based on LAG count (x-axis) against femur length (y-axis) to see if our inferred age was tightly correlated with femur size (the proxy for overall body size), which you can see below.
We had to "adjust" some of the data because there was clear evidence that remodelling had occurred in some individuals, which removes the innermost (oldest) depositions of bone and thus the record of LAGs. There are a number of methods for what's called "retrocalculation," where you attempt to infer how many LAGs have been lost, but they are complicated for small specimens where even a very slight (< 1 mm) difference in plane of section can essentially invalidate these methods, which rely on things like overlaying and measuring diameters. So we used a crude "adjustment" where we added +1 inferred year for any specimen in which there was clear remodelling under the assumption that at least one year of growth had been lost; this certainly underestimates some samples, but because we are testing the relationship between size and age, we didn't want to add more missing years to larger specimens because that would bias the data.
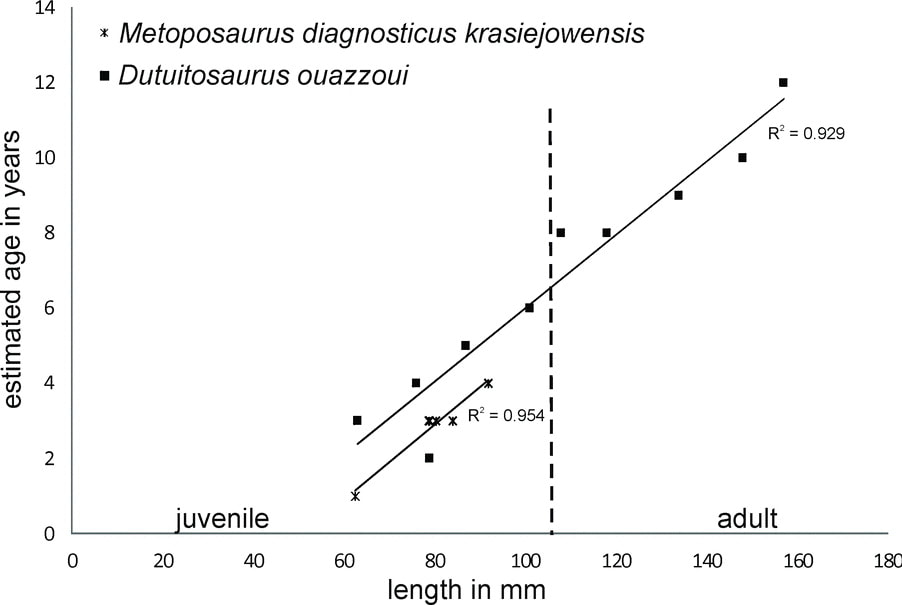
Growth "curves" A growth curve is exactly what it sounds like, and it's definitely supposed to curve. That being said, your data do not always fit to a curve, and they may actually fit to some other fitting model like a straight line or a parabola that don't make much biological sense. Especially with fossils, there can be a lot of reasons for this - some examples can be that you are only sampling part of a growth curve and so you get a section modeled better by another regression or that there are confounding variables that aren't accounted for (e.g., size differences between sexes). The huge spread in our data made this more complicated. Above are some simple model fits using different types of linear models (2nd-order polynomial [parabola], simple linear, exponential, and logarithmic. Why'd we use really simple models? For one, we don't have a lot of other variables to use. In living animals, you can add in body mass, but you can't weigh a dead animal known only from one limb bone, and estimating it is usually done by one of the already existing variables - body size. We also can't control for things like biological sex or contemporaneity (did they live at the same time). So the model almost certainly underfit the data. Apparently the data fit is actually not that bad. For one, it goes in a logical direction (higher body size with increased age), and what we call the r-squared (R^2) value, or the correlation coefficient, is not that bad. It's important to note though that a high correlation does not equate to a high biological accuracy. We could get a perfect fit with a...51-order polynomial (x^51) because that would create a parameter for every single data point we could include. Statistical significance =/= biological significance.
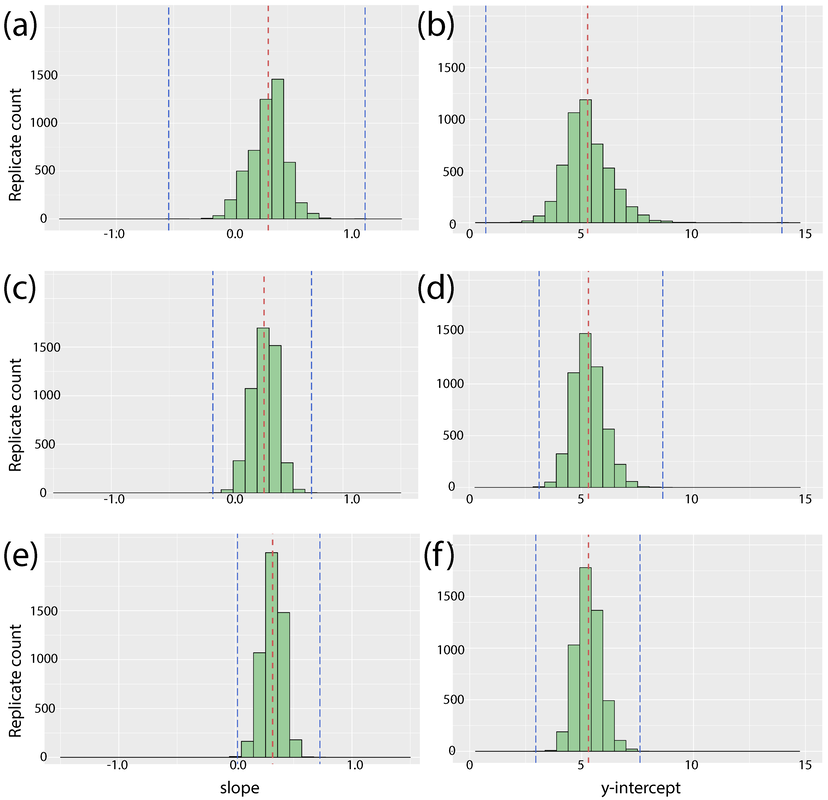
Sample size Sample size is everything in science. If you only have one observation, how much can you really say about a question or a phenomenon? Well, really you can say anything you want (and we often do in paleontology), but how robust or well-supported what you say is more up for debate. What we did here is a series of sensitivity analyses to look at how small sample sizes affect the observed correlation between body size and inferred age. Of the 52 samples that we got LAG counts for, we subsampled in size bins of 10, 20, and 30 (essentially jackknifing the data) where a code would randomly grab X number of data points, plot them, and calculate the regression for those select points (we just used a simple linear model because the model choice wasn't super important for this particular part of the study). When you code this in R, you can run a for loop to do this for however many iterations you want to do it quickly (we did 5,000). We then pulled each variable (y-intercept, slope, correlation coefficient) from each iteration and then produced a histogram of each variable. You can see these below; from left - correlation coefficient (r-squared); slope; y-intercept. What we found is that the extremes are way more likely in low sample sizes (look at the spread for the size bin of 10 for correlation coefficient on the left). Now this isn't surprising or novel on its own; low sample size is more susceptible to confounding variables that aren't being modeled. However, our analysis demonstrates just how wild it can get. The mean (average) value changes little with sample size, but the range of possible outcomes changes massively (marked by dashed blue lines). For n = 10, it was possible to get:
Refs
David Marjanović
2/7/2020 01:09:09 pm
A good paper and a good blog post!
David Marjanović
2/7/2020 01:10:14 pm
Oh, I forgot: Comments are closed.
|
About the blogA blog on all things temnospondyl written by someone who spends too much time thinking about them. Covers all aspects of temnospondyl paleobiology and ongoing research (not just mine). Categories
All
Archives
January 2024
|




 RSS Feed
RSS Feed
